(+)분류 : 가져온 문서/오메가
Regular Polyhedron
점추이적이면서 모든 면이 정다각형인 다면체, 즉 모든 점에 대해 동일한 정다각형이 동일한 갯수만큼 모여서 만들어진 볼록 다면체를 의미한다.
1. 역사 ✎ ⊖
볼록 정다면체는 예전부터 알려져 있었고, 피타고라스 학파가 정십이면체를 발견했다고 한다. 볼록 정다면체가 플라톤 입체라고 불리우는 이유는, 플라톤이 이 다섯 볼록 정다면체를 우주의 원소와 우주에 대응시킨 철학을 발전시키고자 했기 때문이다. 오목 정다면체는 케플러가 두 개를 발견했고 푸앵소가 나머지 두 개를 발견했으며, 이들을 케플러-푸앵소 다면체라고 부른다.
2. 정다면체의 목록 ✎ ⊖
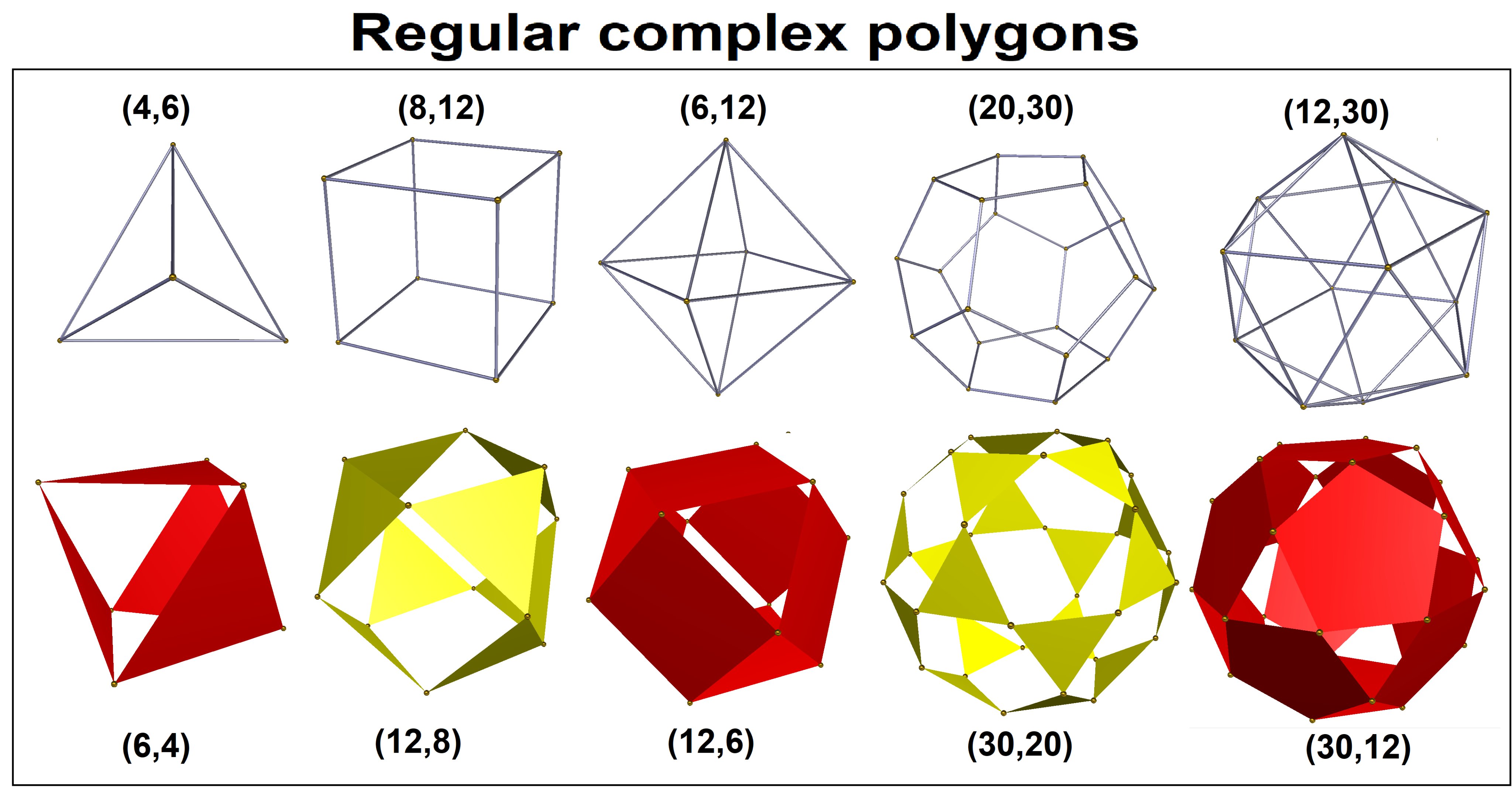
| 이름 | 면 | 변 | 꼭지점 | 면의 모양 | 꼭지점의 면 수 | 대칭군 |
| 정사면체 | 4 | 6 | 4 | 3 | 3 | Td |
| 정육면체 | 6 | 12 | 8 | 4 | 3 | Oh |
| 정팔면체 | 8 | 12 | 6 | 3 | 4 | Oh |
| 정십이면체 | 12 | 30 | 20 | 5 | 3 | Ih |
| 정이십면체 | 20 | 30 | 12 | 3 | 5 | Ih |
3. 군과의 연관성 ✎ ⊖
리 군에서 산발적인(sporadic) 군과 정십이면체, 정이십면체가 관련이 있다.

